Lecture 6 - Dynamic Programming Application - Edit Distance

Attribution

Much of the content from these notes is taken directly or adapted from the notes of the same course taught by Dr. Andrew Forney available at forns.lmu.build.

Introduction

By now, we’ve seen a couple of different applications of dynamic programming with Changemaking and Longest Common Subsequence (LCS). We’ll take a look now at one more example that we use on a daily basis: spelling correction.

Take a look at the example from Microsoft Word with the word “intentionally” misspelled:

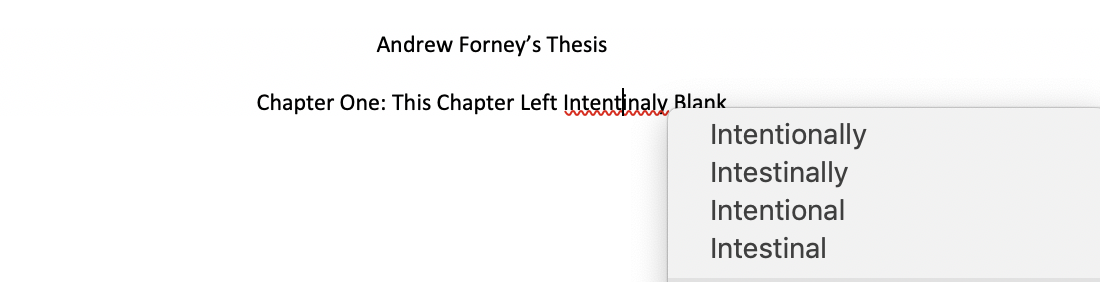
Question

How do you think the suggested words are selected in the spelling correction feature of Microsoft Word?

Intuitively, the “closest” words to the misspelled word are suggested. To define this closeness, we need a metric of “difference” between two strings. It turns out that we can draw inspiration from the Longest Common Subsequence (LCS) problem to define this metric.

The Edit Distance between two strings is the minimal number of primitive string-manipulations that are required to turn one string into another.

Question

What are some common mistakes that people make when misspelling words?

Some common mistakes might include adding an extra letter, missing a needed letter, putting the wrong letter where another belonged, and swapping the positions of two adjacent letters.

Formally, we’ll consider the following primitive string-manipulations:

1. Deletion: Remove a letter from the string.
2. Insertion: Add a letter to the string.
3. Replacement: Replace a letter in the string with another.
4. Transposition: Swap the positions of two adjacent letters in the string.

We’ll consider each of these operations to have a uniform cost.

Some examples of primitive string transformations are shown below:

// Deletion
DRINKE -> DRINK

// Insertion
MRE -> MORE

// Replacement
OVEL -> OVAL

// Transposition
TENE -> TEEN

All of the above examples have an edit distance of 1, as they require a single manipulation to transform the typo into a word.

In practice, we’ll need to string these together for potentially multiple typos. For example, consider the edit distance to turn the string “fkc” into “hack”:

FKC→HKC→HAKC→HACK

The total edit distance $\text{dist}(\text{"FKC"},\text{"HACK"})$ here is 3 for the actions: replacement $F\to H$, insertion $+A$, then transposition $KC\to CK$.

Edit Distance Memoization Structure

We can use dynamic programming to solve the edit distance problem. The memoization structure looks almost exactly the same as with LCS: with one “start” string along one axis and the other “destination” string along the other.

The idea is that we’ll count the minimal number of our 4 primitive operations required to turn the “start” string into the “destination” one.

Let’s take a closer look at the example “fkc” and “hack”. The table structure will look the same as with LCS, but with a slightly different base case configuration around the gutters.

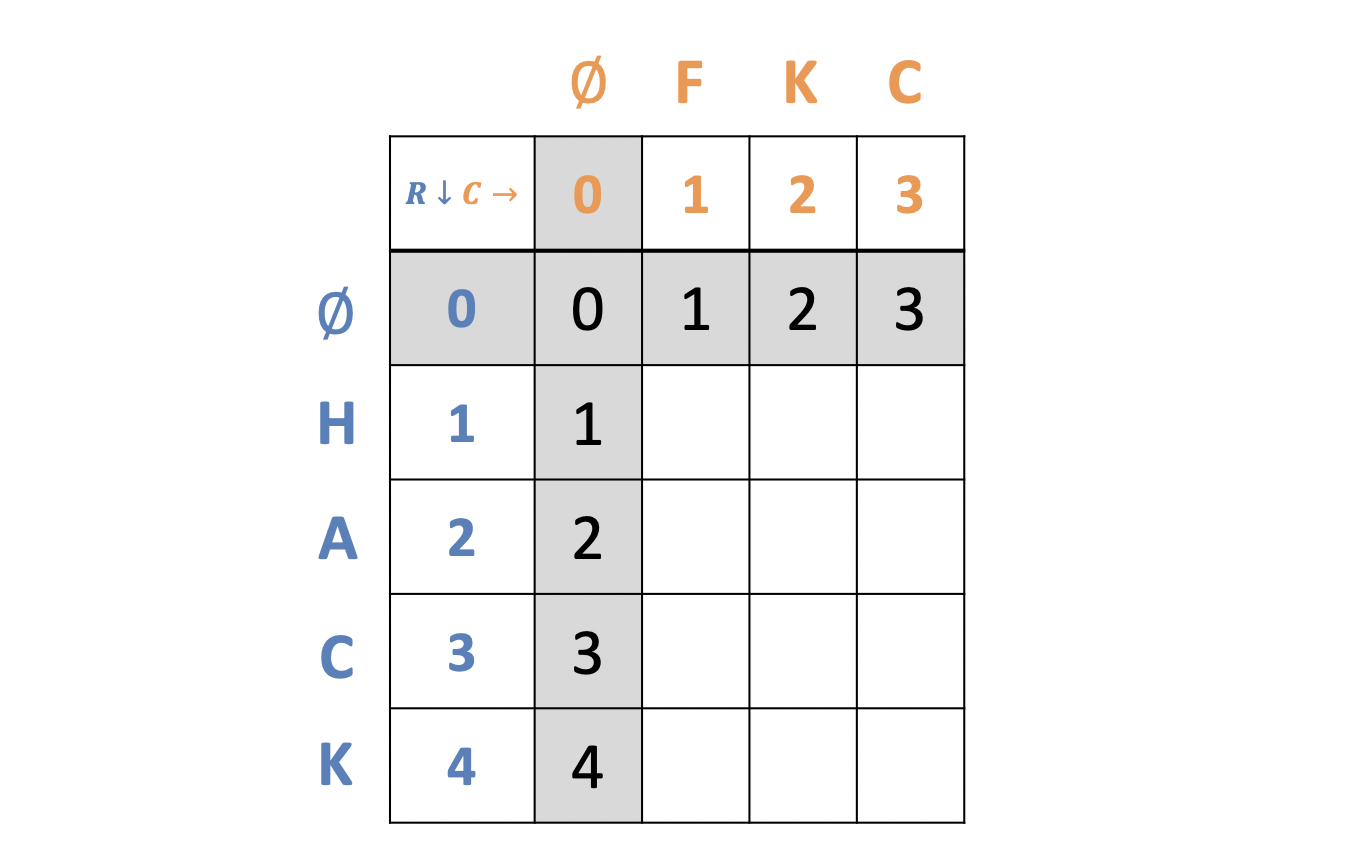
Question

Why do the gutters contain the numbers they do?

Each cell contains the number of letters that would be needed to be removed/added to get from each string to the empty string. These gutters now serve as our base cases for the recurrence that follows.

Edit Distance Recurrence

With the base case out of the way, we’re going to borrow the notation from LCS to think about the recursive cases.

• $r,c$ (lowercase) as the numerical index in each column/row.
• $R,C$ (uppercase) as the strings along the rows and columns, respectively.
• $R[r],C[c]$ the “newly added” characters at row $r$ and column $c$ in strings $R$ and $C$, respectively.
• $R[0,r],C[0,c]$ indicating the prefixes/substrings of length $r,c$ in each of the row and column strings, respectively.
• $T[r][c]$ the value in the table at row $r$ and column $c$, which should contain an integer indicating the minimum number of operations required to turn the column substring $C[0,c]$ into the row substring $R[0,r]$ (or vice versa, since edit distance is symmetrical).

Some intuitions for the recurrence:

• Since we’ve ordered the table with smaller sub-problems above and to the left of any cell, our recurrence must only reference those.
• We’re going to examine only the most recently “appended” characters to each of the row and column strings as a way of working backwards to the base case.

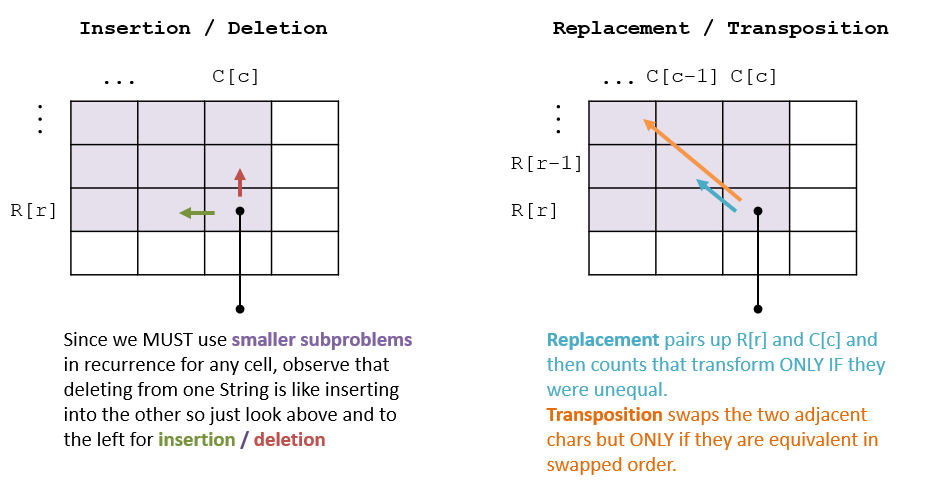
Our goal is to take the minimum edit distance from the edit-path corresponding to each of the 4 string operations:

$$T[r][c]=\min \{\begin{array}{ll}\text{Deletion Case},& \text{if }r\ge 1\\ \text{Insertion Case},& \text{if }c\ge 1\\ \text{Replacement Case},& \text{if }r,c\ge 1\\ \text{Transposition Case},& \text{if }r,c\ge 2\end{array}$$

Here’s a summary of the edit distance recurrence:

Case	Description	Recurrence
Insertion	Adding 1 character to $C$, so add 1 to column from left	$T[r][c-1]+1$
Deletion	Removing 1 character from $R$, so add 1 to row above	$T[r-1][c]+1$
Replacement	Making $C[c]=R[r]$, which only has some cost if they are not already equal	$T[r-1][c-1]+(C[c]\ne R[r])?1:0$
Transposition	Only possible if the two adjacent characters are equal but swapped	$T[r-2][c-2]+1$ if $R[r]=C[c-1]$ and $C[c]=R[r-1]$

Let’s see the full example of the edit distance between the strings “fkc” and “hack”:

As we can see, the edit distance between the two strings is, in fact, 3!

Extra Practice

Before looking at the answer below, try to find the edit distance between the strings “WXYYXW” and “WYXXYX”.

In practice, many spell correctors will pick an arbitrary edit-distance cutoff of around 2-3 and then only examine those words in the dictionary that can be reached up until that edit distance.

That’s why, when you really mess up a word, your computer might not be able to suggest a correction. There are other techniques for spelling correction not covered here, but edit distance is a good tool to have in your back pocket for many string-distance tasks!